I. Các định nghĩa về ma trận:
1. Định nghĩa 1.1:
Một ma trận A loại (cấp) m x n trên trường K (K – là trường thực R, hoặc phức C) là một bảng chữ nhật gồm m x n phần tử trong K được viết thành m dòng và n cột như sau:
Trong đó  là phần tử ở vị trí dòng i, cột j của A. Đôi khi A được viết ngắn gọn là
là phần tử ở vị trí dòng i, cột j của A. Đôi khi A được viết ngắn gọn là  hay
hay 
Các ma trận thường được ký hiệu bởi A, B, C và tập hợp tất cả các ma trận loại m x n trên trường K được ký hiệu bởi Mm x n(K)
Ví dụ 1.1: 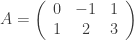 là ma trận cấp 2 x 3.
là ma trận cấp 2 x 3.  là ma trận cấp 3 x 2.
là ma trận cấp 3 x 2.
Ví dụ 1.2: Viết ma trận cấp 4 x 4 biết: 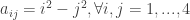
Nhận xét:
– Ma trận A có thể xác định trực tiếp bằng cách liệt kê các phần tử, cũng có thể được xác định theo công thức tổng quát.
– Ma trận không cấp m x n (ma trận zero), ký hiệu 0mxn là ma trận mà mọi phần tử đều bằng 0.
– Nếu m = n thì A được gọi là ma trận vuông cấp n trên K. Tập hợp tất cả các ma trận vuông cấp n trên K được ký hiệu là Mn(K)
– Ma trận cấp 1 x n được gọi là ma trận hàng; ma trận cấp m x 1 được gọi là ma trận cột
– Nếu A là ma trận vuông cấp n, thì đường chứa các phần tử a11, a22, a33,…, ann được gọi là đường chéo chính của A.
2. Định nghĩa 1.2: Cho  . Khi đó:
. Khi đó:
– Nếu 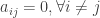 (nghĩa là tất cả các phần tử bên ngoài đường chéo chính của A đều bằng 0) thì ta nói A là ma trận đường chéo.
(nghĩa là tất cả các phần tử bên ngoài đường chéo chính của A đều bằng 0) thì ta nói A là ma trận đường chéo.
– Ta thường dùng ký hiệu diag(a1, a2,…, an) để chỉ một ma trận đường chéo cấp n có các phần tử trên đường chéo lần lượt là a1, a2, …, an
– Ma trận chéo có  (nghĩa là các phần tử trên đường chéo chính đều bằng 1) được gọi là ma trận đơn vị. Ký hiệu: In
(nghĩa là các phần tử trên đường chéo chính đều bằng 1) được gọi là ma trận đơn vị. Ký hiệu: In
– Một ma trận đường chéo với tất cả các phần tử trên đường chéo chính đều bằng nhau được gọi là ma trận vô hướng.
– Nếu  (nghĩa là tất cả các phần tử nằm bên dưới đường chéo chính của A đều bằng 0) thì ta nói A là ma trận tam giác trên.
(nghĩa là tất cả các phần tử nằm bên dưới đường chéo chính của A đều bằng 0) thì ta nói A là ma trận tam giác trên.
– Nếu 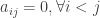 (nghĩa là tất cả các phần tử nằm bên trên đường chéo chính của A đều bằng 0) thì ta nói A là ma trận tam giác dưới.
(nghĩa là tất cả các phần tử nằm bên trên đường chéo chính của A đều bằng 0) thì ta nói A là ma trận tam giác dưới.
– Ma trận tam giác trên hay tam giác dưới được gọi chung là ma trận tam giác.
II. Các phép toán trên ma trận:
1. Định nghĩa 2.1 (hai ma trận bằng nhau):
Cho.
Ta nói A = B khi và chỉ khi:
Ví dụ: Với  Thì
Thì 
Hai ma trận  không thể bằng nhau do không cùng cấp.
không thể bằng nhau do không cùng cấp.
2. Định nghĩa 2.2 (Ma trận chuyển vị):
Cho  . Ta nói:
. Ta nói:
Ví dụ: Nếu  thì
thì 
3. Tính chất 2.1:
Cho. Khi đó:
1.2.
Ghi chú:
Cho  . Khi đó, nếu AT = A thì ta nói A là ma trận đối xứng; nếu AT = – A thì ta nói A là ma trận phản xứng.
. Khi đó, nếu AT = A thì ta nói A là ma trận đối xứng; nếu AT = – A thì ta nói A là ma trận phản xứng.
Ví dụ: 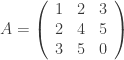 là ma trận đối xứng.
là ma trận đối xứng. 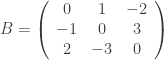 là ma trận phản xứng.
là ma trận phản xứng.
Nhận xét: Nếu B là ma trận phản xứng thì các phần tử trên đường chéo chính của B đều bằng 0.
4. Phép nhân một số với một ma trận:
ChoTa gọi tích a và A (ký hiệu aA) là một ma trận
được xác định bởi:
– Nếu a = -1 thì ta ký hiệu (-1).A bởi -A và gọi là ma trận đối của A.
5. Cộng hai ma trận:
5. Cộng hai ma trận:
ChoTa gọi tổng của A và B (A + B) là một ma trậnđược xác định bởi:
Tổng của A + (-B) được ký hiệu bởi A – B và gọi là hiệu của ma trận A và B.
6. Tính chất 2.2:
6. Tính chất 2.2:
Cho 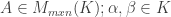 . Ta có: (ab).A = a.(bA); (aA)T = a.(AT)
. Ta có: (ab).A = a.(bA); (aA)T = a.(AT)
7. Ví dụ: Xác định các giá trị của x, y sao cho:
8. Định lý 2.1:
Cho. Khi đó:
1.Tổng hai ma trận có tính giao hoán: A + B = B + A2.Tổng hai ma trận có tính kết hợp: A + (B + C) = (A + B) + C3.Tồn tại ma trận 0mxn sao cho: A + 0 = 0 + A = A4. Tồn tại ma trận đối của A sao cho: A + (- A) = (- A) + A = 05.Phép nhân vô hướng có tính phân phối: α(A+B) = αA + αB ;(α +β)A = αA + βA6.Chuyển vị của tổng bằng tổng các chuyển vị:(A + B)T = AT + BT

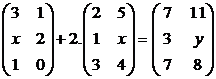
Đăng nhận xét